√70以上 x y/2=4 x/3 2y=5 by cross multiplication method 873422

 Find an answer to your question By using cross multiplication method find x/22y/3=1 and xy/3=3 ramaanjaneyulu2 ramaanjaneyulu2 Math Secondary School answered By using cross multiplication method find x/22y/3=1 and xy/3=3 2 See answers nihithsk23p8phh5 nihithsk23p8phh54 4 x = 4 Substitute 4 for x in either x – 3y = 7 original equation Then solve for y 4 – 3y = 7 – 3y = 3 3y = 3 3 3 y = –1 Use elimination to solve each system of equations 1 2x 2y = –2 2 4x – 2y = –1 3 x – y = 2 3x – 2y = 12 –4x 4y = –2 x y = –3 ( , ) ( , ) ( , ) 4 6x 5y = 4 5 2x – 3y = 12Is done on EduRev Study Group by Class 10 Students The Questions and Answers of 04x 03y=17 07x02y=08 7 (y 3)2 (X 2)=14 4 (y2) 3 (x3)=2 X y/2=4 X/3 2y=5 solve this in two min

Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo

X y/2=4 x/3 2y=5 by cross multiplication method

X y/2=4 x/3 2y=5 by cross multiplication method-Class 10 Maths Linear Equations in 2 Variables Cross Multiplication Method Cross Multiplication Method Let's assume that we have to find solution for a 1 x b 1 y c 1 = 0 (i) and a 2 x b 2 y c 2 = 0 (ii) Step 1 Multiply Equation (i) by b 2 and Equation (ii) by b 1, to get b 2 a 1 x b 2 b 1 y b 2 c 1 = 0 (iii)Assume that x unequals 2,3,4 Then we are allowed to divide both sides by (x2)(x3)(x4) We get (x1)=(x5) 1=5 which is a contradiction so, at least under our assumption there exist no fitting x hm the only x values we didn't try were x=2,3,4 Simply try putting them in the equation and you will see they all work!

Pair Of Linear Equations In Two Variables

Click here👆to get an answer to your question ️ Find the value of x and y using cross multiplication method 3x 5y = 17 and 2x y = 9X = 3 y = 2 Stepbystep explanation multiply the first equation with 2 and second equation with 3 value of y will be equal then you will get value of x put this value of x in any of the equation then get ySolve the equations using the cross multiplication method 3x 2y = 10 and 4x − 2y = 4 Get the answer to this question and access other important questions, only at BYJU'S

So there is exactly one negative solution to the equation When x=1, the y=x^2 curve is at the point y=1, and the y=2^x curve is at y=1/2, so here the y=x^2 curve is already above the y=2^x curve, so they have already crossed This means that they cross at a point between 1 and 0 Now you have two choices to find the value of that numberGiven equation are 6x 7y 11 = 0 and 5x 2y = 13 Comparing with a 1 x b 1 y c 1 = 0 and a 2 x b 2 y c 2 = 0, We have a 1 = 6, b 1 = 7, c 1 = 11 and a 2 = 5, b 2 = 2, c 2 = 13 Now, x = ` b_1c_2 b_2c_1 / a_1b_2 a_2b_1 and y = c_1a_2 c_2a_1 / a_1b_2 a_2b_1 ` ⇒ x = ` 7 xx ( 13) 2 xx ( 11 )/ 6 xx 2 For cross multiplication, = 1 Hence, = 1 x = 2 and, = 1 y = 5 Hence, the required solution is x = 2 and y = 5 Question 4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method

Solve the simultaneous equations x^2 2y=9, yx=3 Use the method of substitution to answer this question Step 1 Rearrange one of the equations to find x or y yx=3 y=x3 Step 2 Substitute your y into the first equation x 2 2y=9 x 2 2 (x3)=9 Step 3 Expand the brackets and rearrange to form a quadratic equationTry to understand section 343 Cross Multiplication Method Exercise35 Q1(ii) Check whether the given pair of linear equations has unique solution, no solution, or infinitely many solutions In case, there is a unique solution, find it by using cross multiplication method 2xy=5 , 3x2y=8Examples on Cross Multiplication Method Example 1 Help Fredie to solve the following pair of linear equations by crossmultiplication 2x5y−52 = 0 3x−4y14 = 0 2 x 5 y − 52 = 0 3 x − 4 y 14 = 0 Solution The terms below x, negative y, and 1 are calculated below Thus, the solution is

Solving Simultaneous Linear Equations By Cross Multiplication Ck 12 Foundation

X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube

3x2y=4 Geometric figure Straight Line Slope = 3000/00 = 1500 xintercept = 4/3 = yintercept = 4/2 = 2/1 = 0000 Rearrange Rearrange the equation by subtractingX/3 y/12 = 19/4 asked in Linear Equations by Anika01 ( 571k points) pair of linear equations in two variables3x 2y = 4 (ii) (I) By substitution method From equation (ii), we have 2y = 4 3x Substitute this value ofy in equation (i), we get Substituting this value of x in equation (iii), we get So, the solution of the given pair of linear equations is x = 2,y = 5 (II) By crossmultiplication method Let us write the given pair of linear

Class Ten Maths Ncert Chapter 3 Solutions Freeguru Helpline

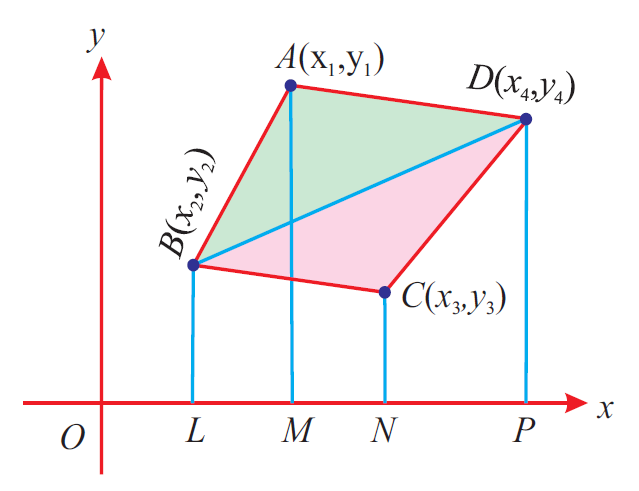
Area Of Quadrilateral When Four Vertices Are Given

 x = 4, y = 1 WARNING! Solve the following pair of linear equation by cross multiplication method x/3 y/12 = 19/4; Use method of crossmultiplications to solve ` 2x y = 8 and 3x 2y = 5`

Solve X Y 7 And 3x 2y 11

8x 5y 9 And 3x 2y 4 By Cross Multiplication Method Brainly In

3x – 3y – 15 = 0 Solution (i) For x – 3y – 3 = 0, 3x – 9y – 2 = 0 ∴ a 1 = 1, b 1 = – 3, C 1 = – 3, a 2 = 3, b 23x 4y 65 =0 asked in Mathematics by sforrest072 ( 128k points) pair of linear equations in two variables Step deviation Method for Finding the Mean with Examples;

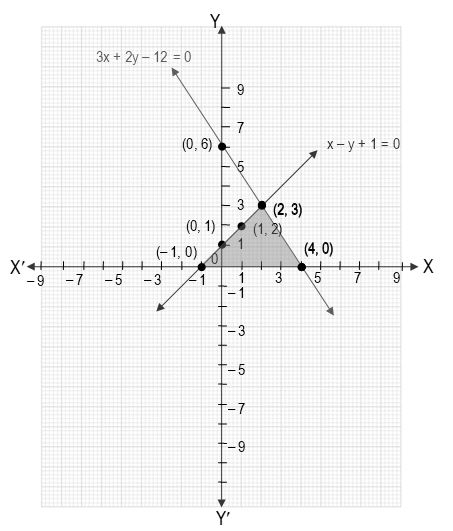
Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community

Solve This By Cross Multiplication Method 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Mathematics Topperlearning Com K2zyk5cc

There Are Actually 4 methods of solving this We have, 2x 3y = 11(i) and, 5x 2y = 18(ii) i) Elimination Method First choose which variable you want to eliminate I'm going with y So, Multiply the eq(i) with 2 first It will turn into, 4x 6y = 22(iii) Now, Multiply the eq(ii) with 3To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Solve by cross multiplication `x2y1=0 `, `2x3y12=0`3x – 9y – 2 = 0 (ii) 2x y = 5;

Algebra 2 Solutions Pdf Integer Rational Number

2

 Ex 35 Class 10 Maths Question 1 Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions In case there is unique solution, find it by using crossmultiplication method (i) x – 3y – 3 = 0, 3x – 9y – 2 = 0 (ii) 2x y = 5, 3x 2y = 8 (iii) 3x – 5y = , 6x – 10y = 40 Solve the linear equations x y = 5, x – y = 3 by using the cross multiplication method? Ex 35, 3 (Substitution method)Solve the following pair of linear equations by the substitution and crossmultiplication methods 8x 5y = 93x 2y = 48x 5y = 93x 2y = 4From (1)8x 5y = 98x = 9 – 5y x = ((9 − 5𝑦))/8Putting value of x in (2)3x 2y = 43 (((9 (टीचू)

2

2

 Solve(cross multiplication method) 2/x3/y=2 1/x1/2y=1/3 Maths Linear Equations in Two VariablesGet stepbystep solutions from expert tutors as fast as 1530 minutes Cross Multiplication Method → FacebookWhatsapp Transcript Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 22(x y) = 2 × 52x 2y = 10 Solving (3) and (2) by Elimination–5y = –6 5y = 6 y = 𝟔/𝟓Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x

Coss Multiplication Method For Solving Linear Equations Ncert 10

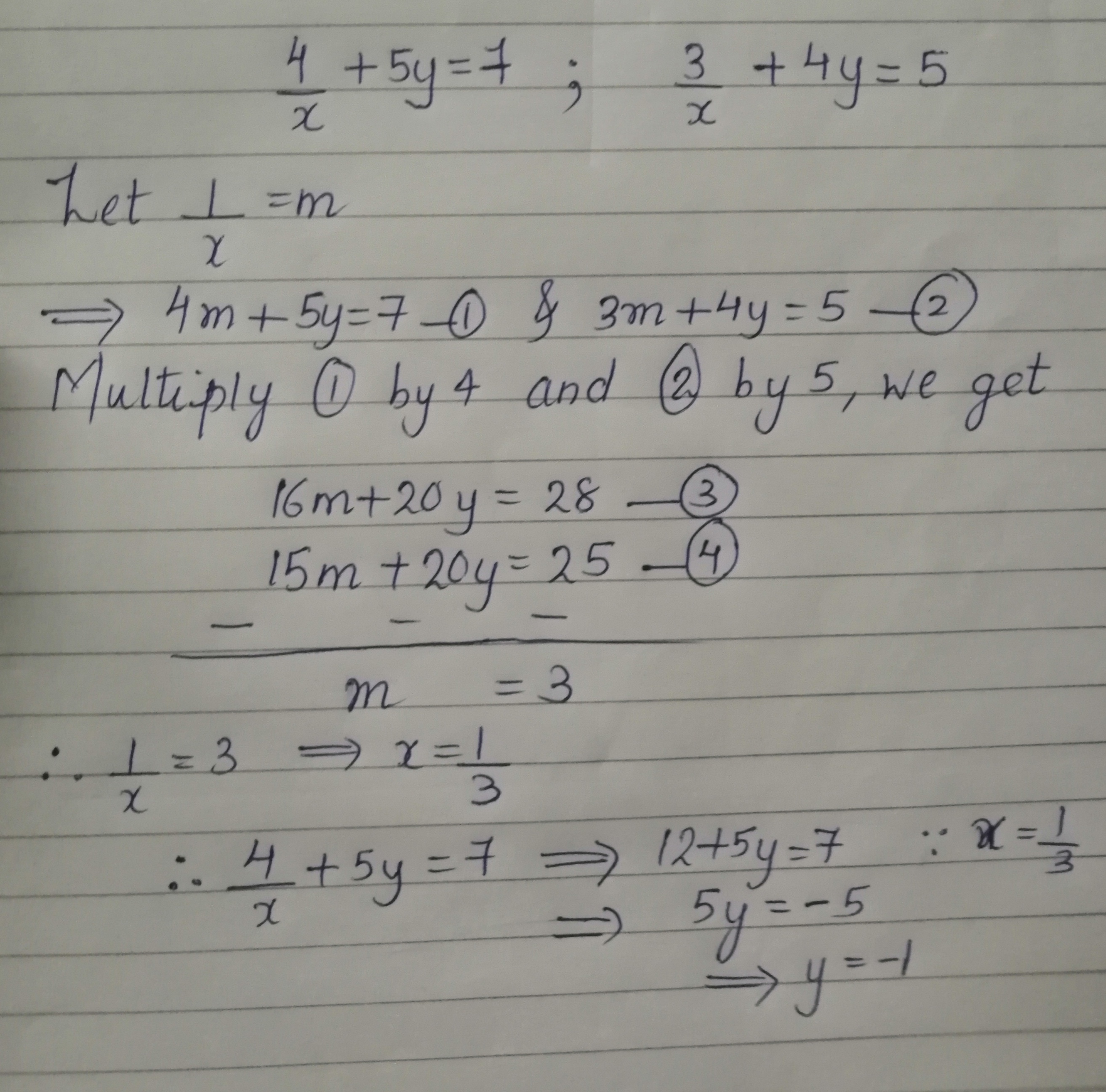
4 X 5y 7 3 X 4y 5 Mathematics Topperlearning Com Eyz2xh55

Theorem The tangent at any point of a circle is perpendicular to the radius through the point of contact Circles Class 10 Maths a 2 = 3, b 2 = 5, c 2 = 4 Now by using cross multiplication we get x/(b 1 c 2 – b 2 c 1) = y/(c 1 a 2 – c 2 a 1) = 1/(a 1 b 2 – a 2 b 1)6x 10y = 40 (iv) x – 3y – 7 = 0; solve using cross multiplication method 2x=5y4 3x2y16=0 Share with your friends Share 1 Answer We know if we x = b 1 c 2 b 2 c 1 a 1 b 2 a 2 b 1 and y = c 1 a 2 c 2 a 1 a 1 b 2 a 2 b 1 Here we have equations 2 x 5 y 4 = 0 and 3 x 2 y 16 = 0 So, a 1 = 2

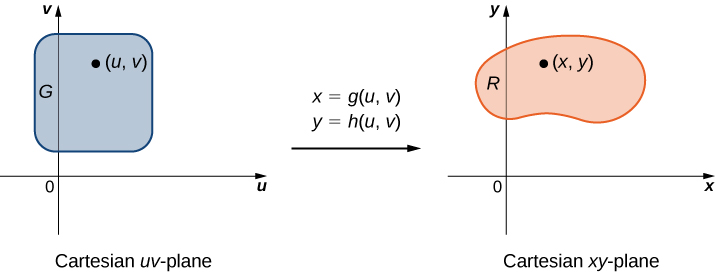
Change Of Variables In Multiple Integrals Calculus Volume 3

Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community

Why do they workSimplify algebraic expressions stepbystep \square!X y = 5 and x – y = 1 Again we get a set of two linear equations with two variables Solve again to find the value of x and y Rearranging them again, x y – 5 = 0 (3) x – y – 1 = 0 (4) From equation (3) a 1 = 1, b 1 = 1 and c 1 = – 5 From equation (4) a 2 = 1, b 2 = – 1 and c 2 = – 1 Using cross multiplication method,

Cross Multiplication Method For Solving Equations A Plus Topper

Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations

3x 2y = 8 (iii) 3x – 5y = ;NCERT Solutions for Class 10 Maths Chapter 3 Exercise 35 Question 3 Summary On solving the following pair of linear equations by the substitution and crossmultiplication methods 8x 5 y = 9 and 3x 2 y = 4 we get x = 2, and y = 5Solution Given system of linear equations are x y = 5 x – y = 3 On transposition, we get x y – 5 = 0 x – y – 3 = 0 Writing the coefficient in the following way, we get By crossmultiplication method

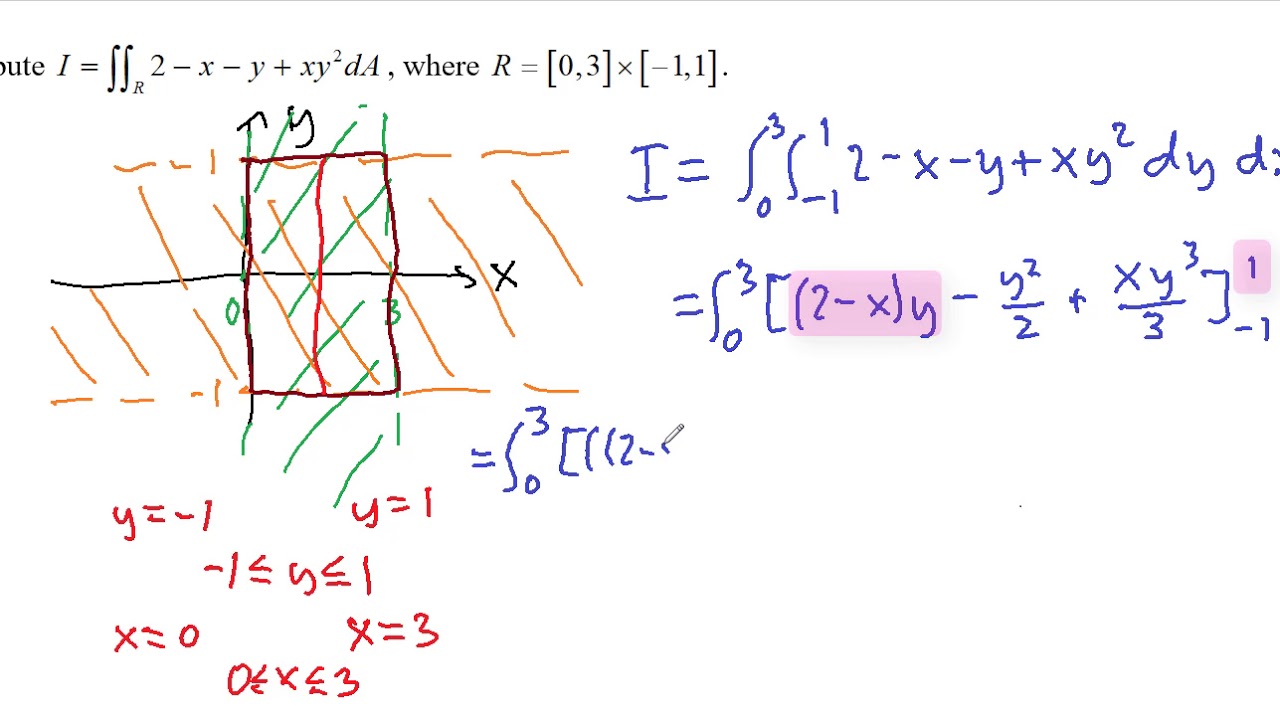
Double Integrals Volume And Average Value

Solve The Following Pair Of Equations By Cross Multiplication Rule 5x 3y 35 2x 4y 28 Then

 Using matrix method, solve the system of equations 3x 2y 2z = 3, x 2y 3z = 6, 2xy z = 2 asked in Class XII Maths by rahul152 Expert ( Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 313 Question 1 Solve by crossmultiplication method Question 2 Akshaya has 2 rupee coins and 5 rupee coins in her purse If in all she has 80 coins totalling Rs 2, how many coins of each kind does she have Let the number of 2 rupee coins be "x" and the number of 5 Now multiply equation (1) by 5 and (2) by 7 By adding both the equations Substitute the value of x in equation (1) Therefore, x = 7 and y = 2 If x = 7 and y – 2 satisfy the equation (3) then we can say that the equations hold simultaneously Substitute the value of x and y in equation (3) 43 = 43 which is true

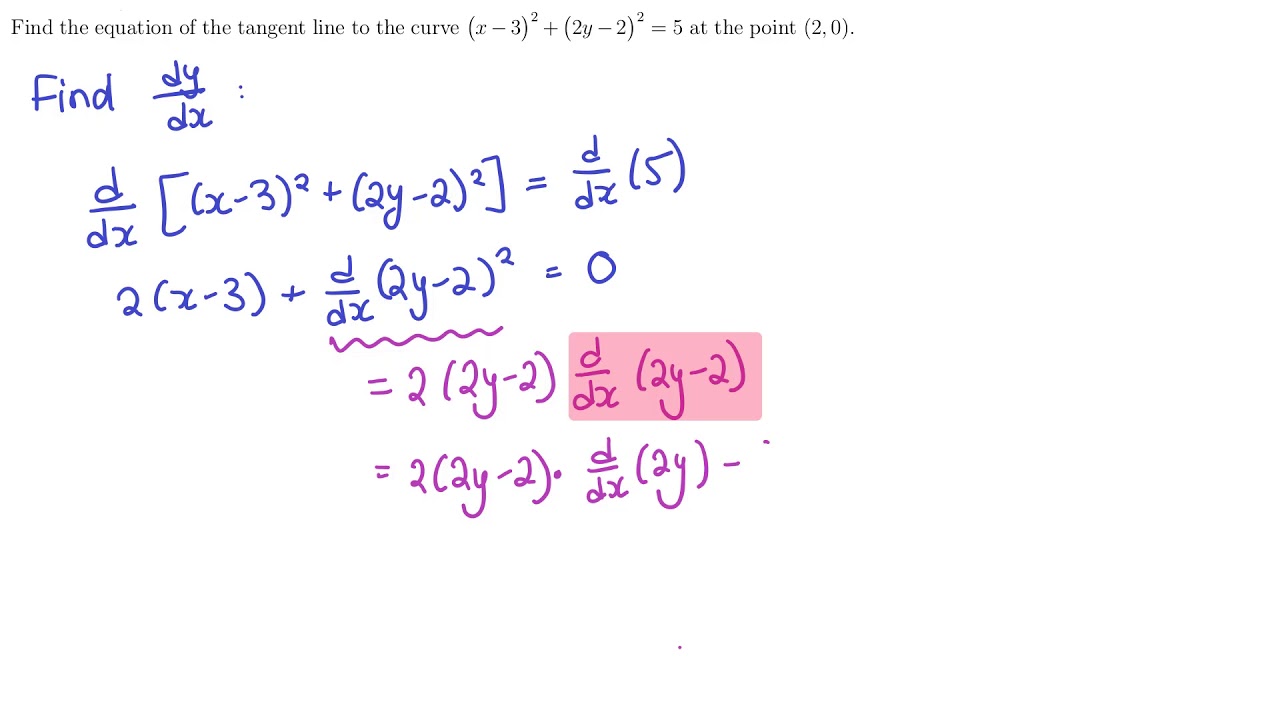
Implicit And Logarithmic Differentiation

Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions

 Solve by Cross multiplication method x2y1=0 and 2x3y12=0X = 1/2, y = 1/3 Hence the solution is (1/2, 1/3) Question 2 Akshaya has 2 rupee coins and 5 rupee coins in her purse If in all she has 80 coins totalling ₹ 2, how many coins of each kind does she have Solution Let "x" and "y" number of 2 rupee and 5 rupee coins respectively x ySimple and best practice solution for xy=6;xy=2 Check how easy it is, to solve this system of equations and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the system of equations solver your own equations and let

5 Ways To Solve For X Wikihow

X 2y 2x 3y 7solve By Cross Multiplication Method Brainly In

 2x5y4=0 3x2y16=0 by crossmultiplication x/b1c2b2c1 = y/c1a2c2a1 = 1/a1b2a2b1 x/808 = y/1232 = 1/415 x/ = y/44 = 1/11 Therefore 1/11 = x/ x=8 1/11=y/44 y=4 From substitution, elimination,and cross multiplication method?Answer (1 of 4) The given simulattaneous equations are 4xy =3 X2y =3 4x3y3=0 (1) x2y3=0 (2) Fo calculating values of xand y of the given equations cross multiplication mehod is used The method name it self indicates cross multiplication Cross multiplication of COEFFICIENT of x

Cross Multiplication Method

Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions

 Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions In case there is a unique solution, find it by using cross multiplication method (i) x – 3y – 3 = 0 3x – 9y – 2 = 0 (ii) 2x y = 5 3x 2y = 8 (iii) 3x – 5y = 6x – 10y = 40 (iv) x – 3y – 7 = 0 3x – 3y – 15 In case there is a unique solution, find it by using cross multiplication method (i) x – 3y – 3 = 0;`x y/2 = 4` (i) `x/3 2y = 5` (ii) From (i), we get `(2x y)/2 = 4` 2x y = 8 y = 8 2x From (ii), we get x 6y = 15 (iii) Substituting y = 8 2x in (iii), we get x 6(8 2x) = 15 `=> x 48 12x = 15` => 11x = 15 48 => 11x = 33 `=> x = (33)/(11) = 3` Putting x = 3 in y = 8 2x we get y = 8 2 x 3 = 8 6 = 2 y = 2

Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths

2

Solve the following system of equations using cross multiplication method (i) 3 x 4 y = 24, x 11 y = 47 Solution (ii) 05 x 08 y = 044 , 08 x 06 y = 05 Solution (iii) (3x/2) (5y/3) = 2 , (x/3) (y/2) = 13/6 Solution (iv) (5/x) (4/y) = 2 , (2/x) (3/y) = 13 Solution Formulate the following problems as a pair of Cross Multiplication Method Examples Example 1 Solve the following system of equations by crossmultiplication method 2x 3y 8 = 0 4x 5y 14 = 0 Sol The given system of equations is 2x 3y 8 = 0 4x 5y 14 = 0 By crossmultiplication, we getTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW 2x 3 y 3z =5 , x 2y z=4 , 3x y2z = 3

Amc Solutions Manual Glenco Solution

Solving Linear Equations By Cross Multiplication Method X 2y 2 X 3y 7 Brainly In

Solve by cross multiplication method 1/2(2x 3y) 12/7(3x 2y) = Ask questions, doubts, problems and we will help youSolve each of the following systems of equations by the method of crossmultiplication 2x y 35=0;The procedure to use the cross multiplication calculator is as follows Step 1 Enter the fractions with the unknown value "x" in the respective input field Step 2 Click the button "Calculate x " to get the output Step 3 The unknown value "x" will be displayed in the output field "x"

無料ダウンロード 3x 2y5 X5 Y

Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy

3x 10 = 4 x = 2 Thus, x = 2 and y = 5 Now, Using Cross Multiplication method 8x 5y – 9 = 0 3x 2y – 4 = 0 x/(18) = y/(27 32 ) = 1/(1615) x/2 = y/5 =1/1 ∴x = 2 and y =5 4 Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method3x2y =10 (1)4x−2y =4 (2)Using formula for cross multiplication method(b1 c2 −b2 c1 )x = (c1 a2 −a1 c2 )y = (a1 b2 −a2 b1 )−1 So, from equation (1) and (2) we can write the value of a,b and c2×4−(−2)×10x = 10×4−3×4y = 3×(−2)−4×2−1 0x = 40−12y = −6−8−1 28x = 28y = −14−1 28x = −14−1 −14x

Coss Multiplication Method For Solving Linear Equations Ncert 10

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4

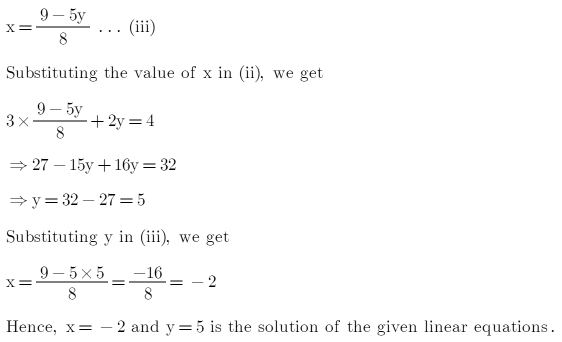
By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll

2

Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo

Solve The Following Pair Of Linear Equations By The Substitution And Cross Multiplication Methods 8x 5y 9 3x 2y 4

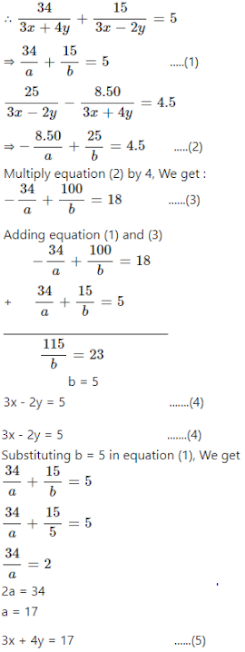
Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths

14 7 Maximum And Minimum Values Mathematics Libretexts

Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15

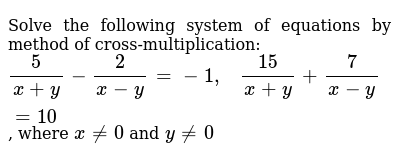
Solve The Following System Of Equations By Method Of Cross Multiplication 5 X Y 2 X Y 1 15 X Y 7 X Y 10 Where X 0 And Y 0

How To Solve By Cross Multiplication For X By 2 Ax By A 4b 0 2 Bx Ay B 4a 0 Quora

Solve By Reducing Them To A Pair Of Linear Equations 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Youtube

Ncert Solutions For Class 10 Maths Chapter 3 Exercise 3 5 Pair Of Linear Equations In Two Variables

Systems Of Linear Equations

How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic

Graph With Intercepts Elementary Algebra

Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations

Solve 3x 2y 12 And 4x Y 5 Using Cross Multiplication Method Brainly In

Multiply 5 X Y X Y 5

2

Row Vector An Overview Sciencedirect Topics

How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic

Systems Of Linear Equations

Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables

Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community

Multiply 5 X Y X Y 5

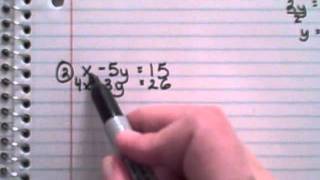
Linear Systems With Multiplication Algebra Socratic

Pair Of Linear Equations In Two Variables

無料ダウンロード 3x 2y5 X5 Y

Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y

2

G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable

3x 4y 10 And 2x 2y 2

Mp Board Class 10th Maths Solutions Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5 Mp Board Solutions

Solve By Cross Multiplication Method 2x 3y 4 0 And 3x 5y 2 0 Brainly In

1

14 5 Directional Derivatives

Ncert Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5 Exercise 3 5

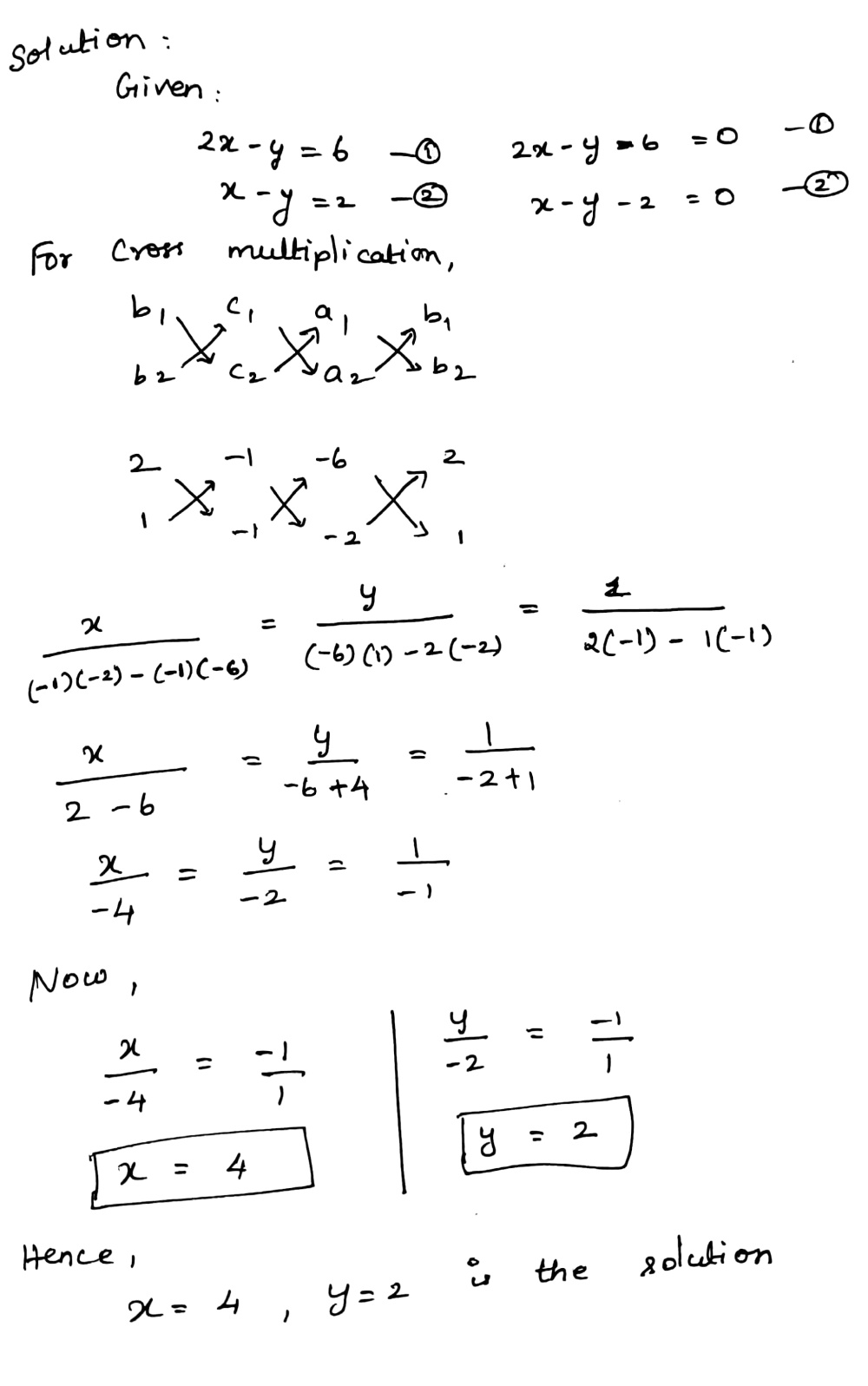
Solve Of The Following Pairs Of Linear Equations By Using Cross Multiplication Method 2x Y 6 X Y 2 Snapsolve

2

Ncert Solutions For Class 10 Maths Chapter 3 Exercise 3 5 Pair Of Linear Equations In Two Variables

How To Solve The Following Pairs Of Equations 7x 2y Xy 5 And 8x 7y Xy 15 Quora

Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15

Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo

Linear Algebra Book Chapter Iopscience

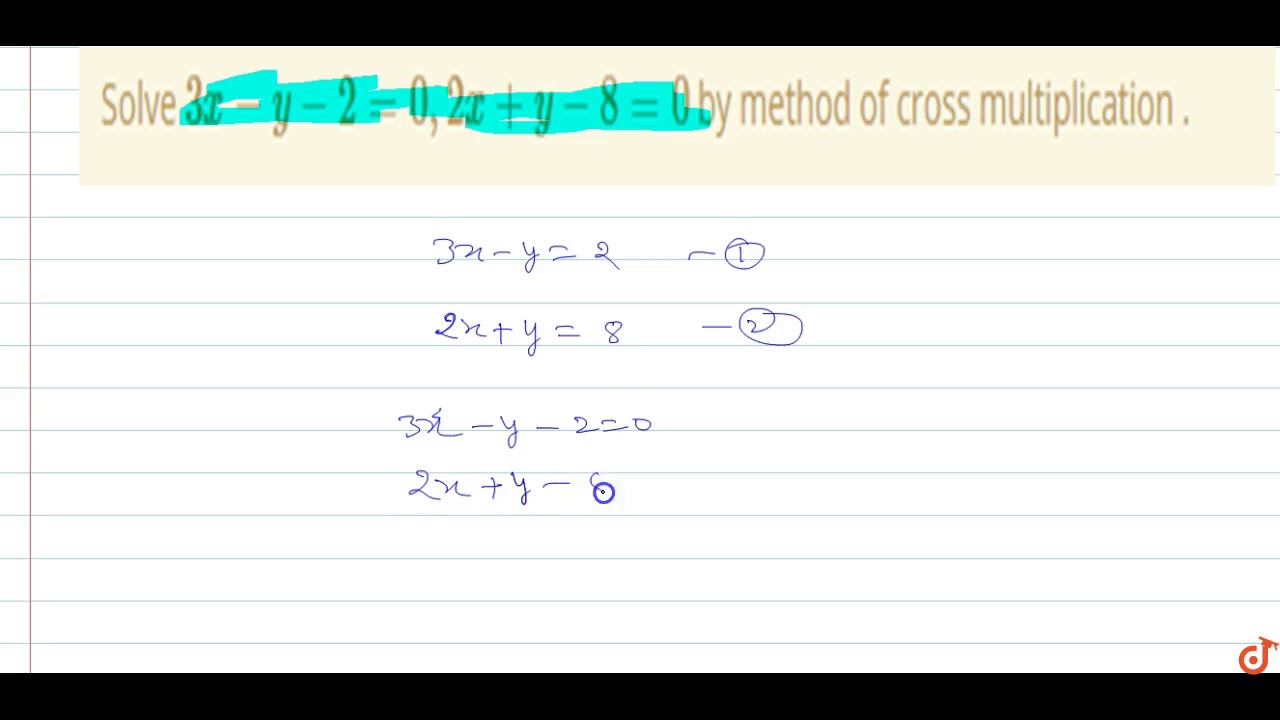
Solve 3x Y 2 0 2x Y 8 0 By Method Of Cross Multiplication Youtube

Solve The Pair Of Linear Equations By Cross Multiplication Method 2 2x Y 5 3 X 3y 1 0 Brainly In

Cross Multiplication Method For Solving Equations A Plus Topper

1

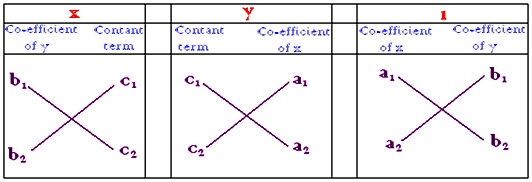
Cross Multiplication Method Formula For Cross Multiplication Linear Equations

2

Solve The Following Systems Of Equations 2 X 3 Y 9 Xy 4 X 9 Y 21 Xy Where X 0 Y 0 Sarthaks Econnect Largest Online Education Community

How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora

Matlab Tutorial

How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora

Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 X 3 Y 12 19 4 Sarthaks Econnect Largest Online Education Community

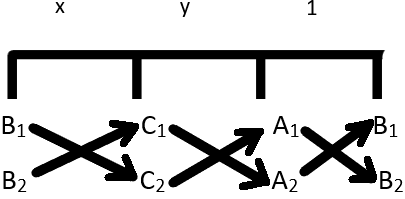
Method Of Cross Multiplication Solve By Method Of Cross Multiplication

Which Of The Following Pairs Of Linear Equations Has Unique Solution No Solution Or Infinitely Many Solutions I X 3y 3 0 3x 9y 2 0

Matlab Tutorial

Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community

How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora

3 Systems Of Linear Equations

Solve The Following Pair Of Linear Equation Bycross Multiplication Method X 2y 2 X 3y 7

無料ダウンロード 3x 2y5 X5 Y

Coss Multiplication Method For Solving Linear Equations Ncert 10

8x 5y 9 3x 2y 4 Solve Using Substitution And Cross Multiplication Method Youtube

R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4

0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question

Is The Pair Of Linear Equations 2x Y 5 And 3x 2y 8 Has Unique Solution In Case There Is A Unique Solution Find It By Using Cross Multiplication Method

Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables

Ncert Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5

Solve For X And Y 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2