70以上 三 平方 の 定理 の ���用 828325

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社

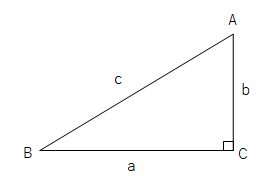
結晶構造の探究 ･･････金児 正史 受験問題に盛り込まれた三平方の定理 ･･････栗田 哲也 和算における三平方の定理 ･･････小寺 裕 文献紹介・三平方の定理の一般化 ･･････古藤 怜 二平方比の定理・三平方比の定理三平方の定理 直角三角形の 3 3 辺の長さには、以下のようの関係式が常に成り立ちます。 a2 b2 = c2 a 2 b 2 = c 2 ※直角三角形の 3 3 辺で、最も長い辺は直角の向かいの辺で、この辺を斜辺といいます。 上の三角形の斜辺は、長さが Ccm C c m の辺です。 なんでこの関係は成り立つの？ という好奇心はちょっと保留して、まずは計算練習をしておきましょう。 例題1 下図の x x を求めなさい。

三 平方 の 定理 の 利用

三 平方 の 定理 の 利用- 三平方の定理は、直角三角形の斜辺の2乗が他の辺の2乗の和に等しい、という公式です。 非常に便利ですが、二次方程式になってしまうので解答するのに時間がかかります。 そこで、テストによく出てくる直角三角形については暗記してしまいましょう。 ここでは、特に重要な7つのパターンをご紹介します。 こちらは非常に有名な直角三角形です。 3つの例3 右図で AC の長さは三平方の定理で求められるが， さらに相似図形の性質を使えば， ACBC=ABx になるので， x が求められる． （相似図形の性質をまだ習っていないときは こちらを先に 読む） 直角三角形 ABC に三平方の定理を適用すると 2152=AC2 AC2

知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より

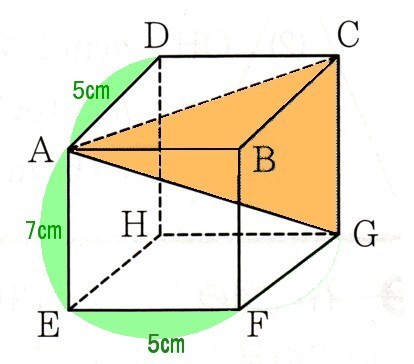
 三平方の定理を利用する難問 1辺が $2$ の正六角形の中心に点Oを取り、その真上の点をPとする。正六角形の各頂点からPまでの長さを $6$ とするとき、OPの長さを求めよ 解説 正六角形の内角の和は7°だよね 補足 n角形の内角の和は、$(n2)\times 180$ だから、底面の正六角形の角度は全て、$7 \div 三平方の定理の利用（立体） 立体や空間図形などでも三平方の定理はよく利用される。 とにかく直角三角形があれば使える定理なので、利用範囲は広くなる。 今回は空間図形で三平方の定理を利用する問題の、もっともシンプルなものを用意した。 直方体の対角線の長さを求めるために三平方の定理を利用する。 二度計算をしなくてはならないため三平方の定理 （さんへいほうのていり） 直角三角形の辺に関する「 ピタゴラスの定理 」のこと 「 三個の平方数の和 」で表される数に関する定理のこと このページは 曖昧さ回避のためのページ です。 一つの語句が複数の意味・職能を有する場合の水先案内のために、異なる用法を一覧にしてあります。 お探しの用語に一番近い記事を選んで下さい

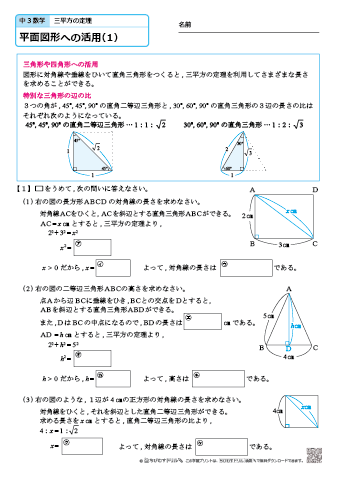
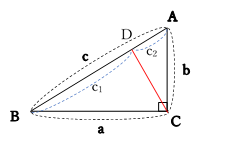
隣にあるのが 隣辺 対面にあるのが 対辺 ですが中学では、「斜辺」と「それ以外」で十分ですね これだけです！ 直角三角形 の3辺のうち、 2辺が判れば残りの1辺がわかります 三平方の定理を少し変形すると c 2 = a 2 b 2 → c = √a2 b2 a 2 b 2 a 2 = c 2 b 2三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 A B 例図の線分ABの長さを求める。 x y O A (2,1) B (7,3) 確認線分ABの長さを求めよ。 A (1,5) B (6,2) x y O B (2,2) A (1, 4) O x y 長方形三平方の定理中学3年生 数学平面図形への利用 11 特別な三角形 111 90°、45°、45° の三角形;

三 平方 の 定理 の 利用のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	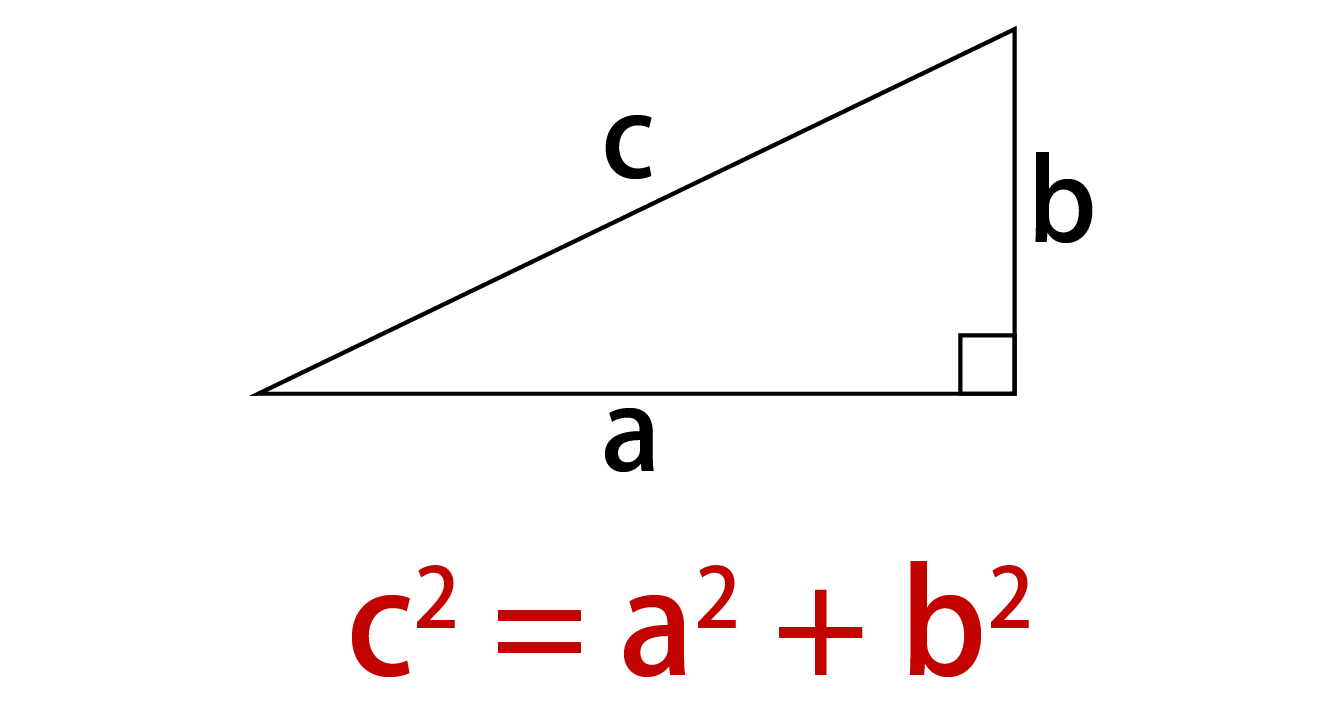三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	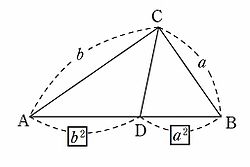三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	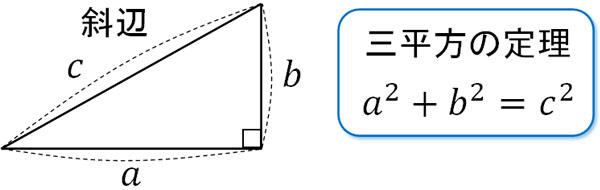三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	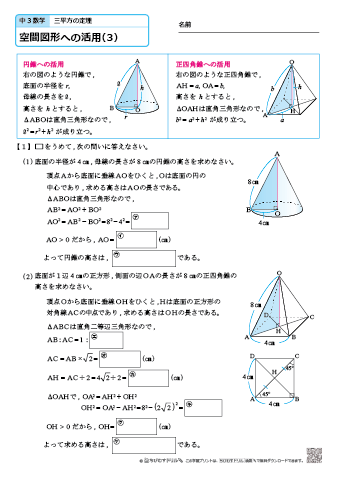三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	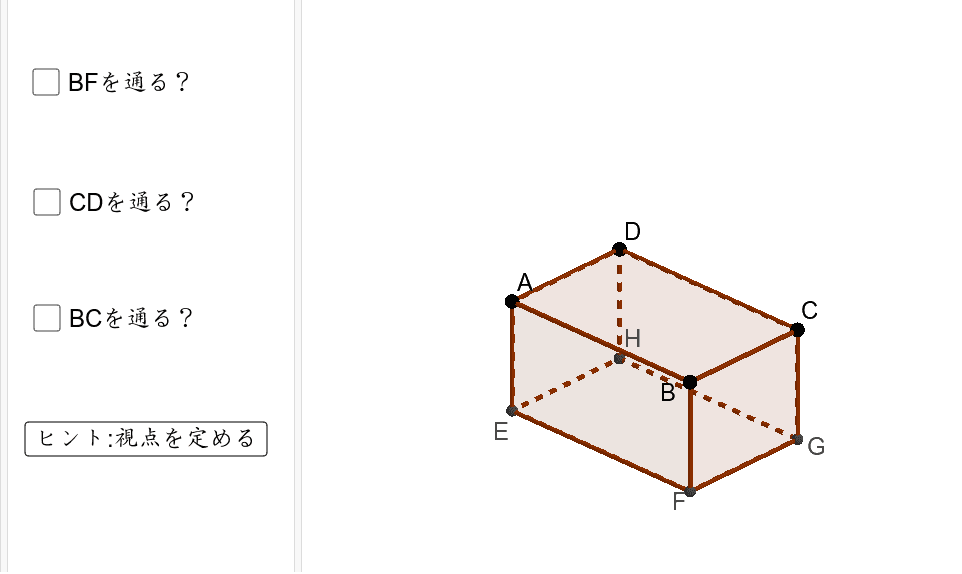三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	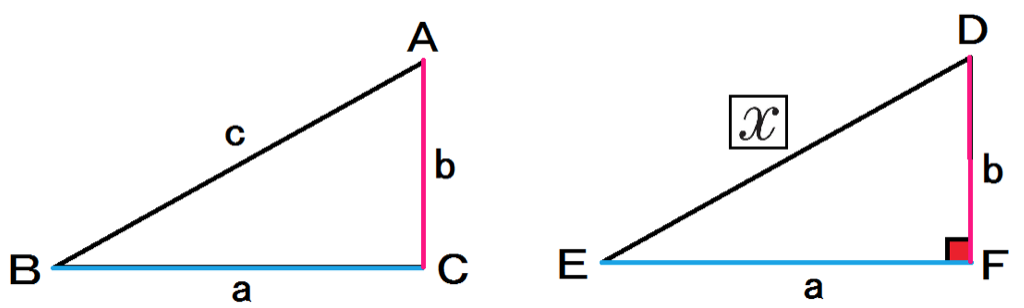三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	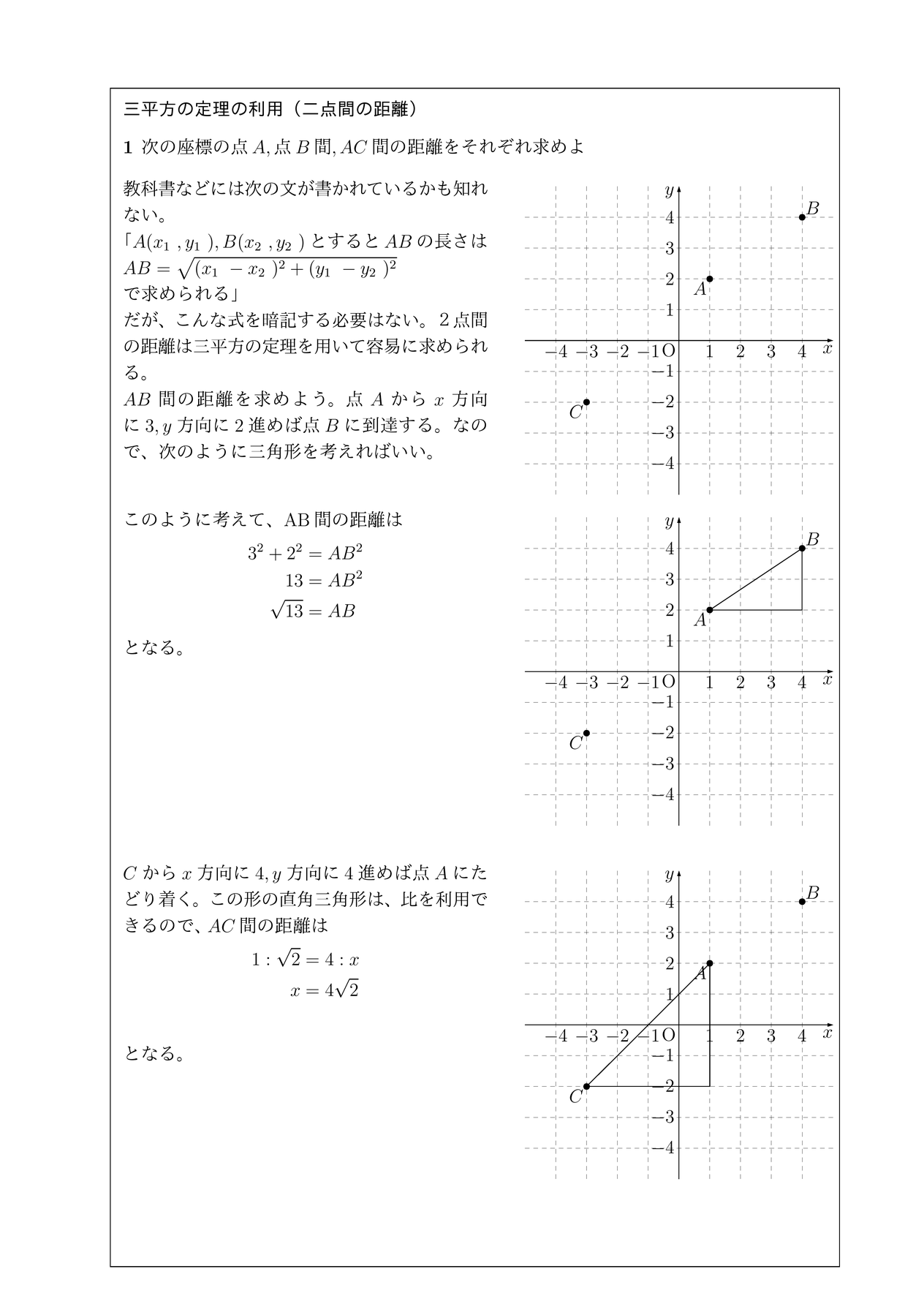三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	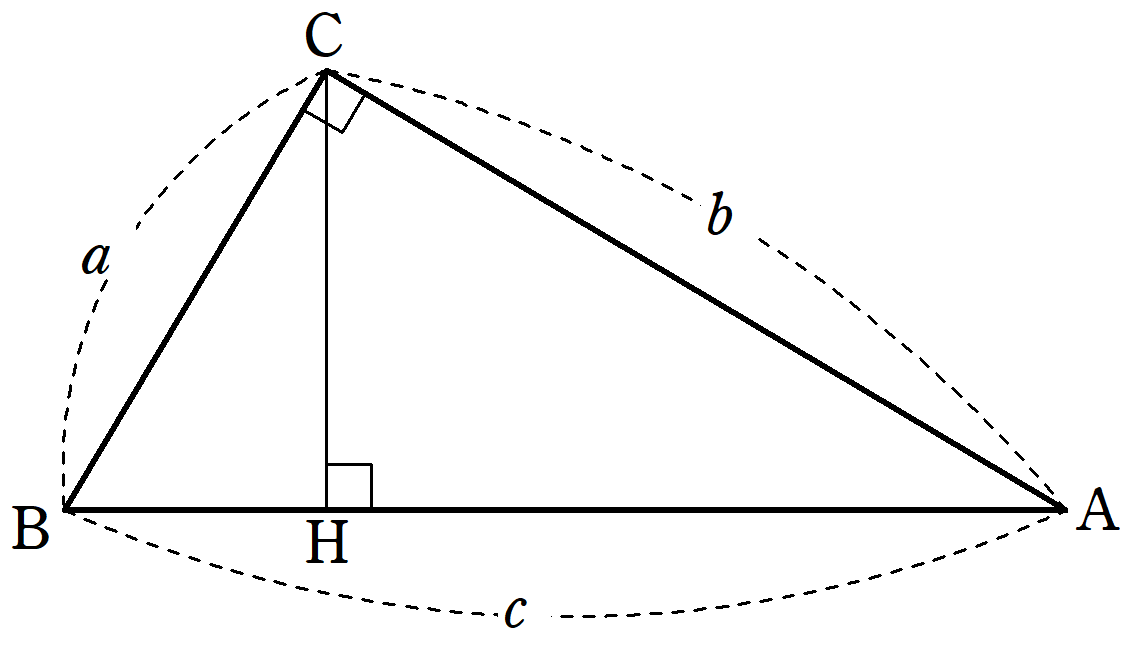三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

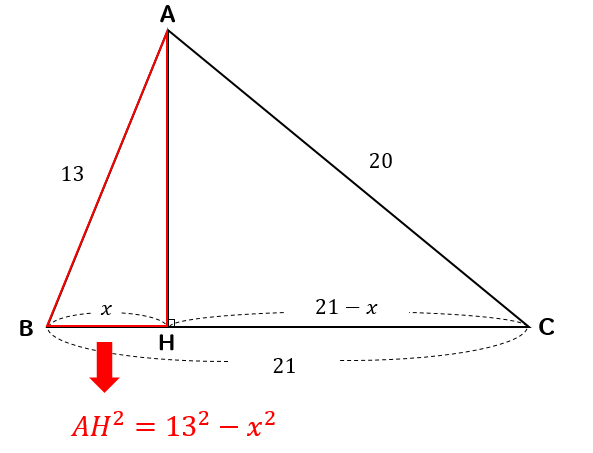
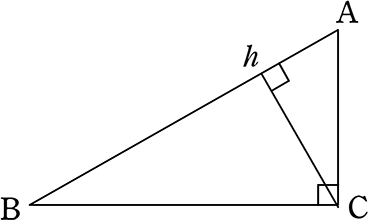
三角錐ebfg と三角錐ebcd の体積比を求めなさい。 (4) 四角錐efcdg と正四面体abcd 体積比を求めなさい。 4㎝ A B E F D G 三平方の定理⑦平面図形への利用（2） a 学 年 3 年 学習日： 月 日（ ） 中学校数学・ワークブック 中学校数学 3b7 －7a 年 組 氏名 解答 年 〔 point 〕 ① 立体の表面直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) x=2 例2 長方形の向かい合う辺の長さは等しいので，次の図で AH=DC になる． この AH の長さと AB の長さから三角形 ABH について三平方の定理を使うと辺 BH が求まり， HC